极客分享
目录

2.记忆化搜索

记忆化搜索实际上是递归来实现的，但是递归的过程中有许多的结果是被反复计算的，这样会大大降低算法的执行效率。

而记忆化搜索是在递归的过程中，将已经计算出来的结果保存起来，当之后的计算用到的时候直接取出结果，避免重复运算，因此极大的提高了算法的效率。

# 例题

在具体讲何为「记忆化搜索」前，先来看如下的例题：

"NOIP 2005 采药 (opens new window)"

  • 山洞里有 株不同的草药，采每一株都需要一些时间 ，每一株也有它自身的价值 。给你一段时间 ，在这段时间里，你可以采到一些草药。让采到的草药的总价值最大。

# DFS 做法

注：为了节省篇幅，本文中所有代码省略头文件。

    int n, t;
int tcost[103], mget[103];
int ans = 0;
void dfs(int pos, int tleft, int tans) {
  if (tleft < 0) return;
  if (pos == n + 1) {
    ans = max(ans, tans);
    return;
  }
  dfs(pos + 1, tleft, tans);
  dfs(pos + 1, tleft - tcost[pos], tans + mget[pos]);
}
int main() {
  cin >> t >> n;
  for (int i = 1; i <= n; i++) cin >> tcost[i] >> mget[i];
  dfs(1, t, 0);
  cout << ans << endl;
  return 0;
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    tcost = [0] * 103
mget = [0] * 103
ans = 0

def dfs(pos, tleft, tans):
    global ans
    if tleft < 0:
        return
    if pos == n + 1:
        ans = max(ans, tans)
        return
    dfs(pos + 1, tleft, tans)
    dfs(pos + 1, tleft - tcost[pos], tans + mget[pos])

t, n = map(lambda x:int(x), input().split())
for i in range(1, n + 1):
    tcost[i], mget[i] = map(lambda x:int(x), input().split())
dfs(1, t, 0)
print(ans)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    // Make sure to add code blocks to your code group

    这就是个十分朴素的大暴搜是吧……

    emmmmmm…… 分。

    # 优化一

    然后我心血来潮，想不借助任何“外部变量”（就是 dfs 函数外且 值随 dfs 运行而改变的变量), 比如 ans

    把 ans 删了之后就有一个问题：我们拿什么来记录答案？

    答案很简单：

    返回值！

    此时 dfs(pos,tleft) 返回在时间 tleft 内采集 后 pos 个草药，能获得的最大收益

    不理解就看看代码吧：

      int n, time;
int tcost[103], mget[103];
int dfs(int pos, int tleft) {
  if (pos == n + 1) return 0;
  int dfs1, dfs2 = -INF;
  dfs1 = dfs(pos + 1, tleft);
  if (tleft >= tcost[pos]) dfs2 = dfs(pos + 1, tleft - tcost[pos]) + mget[pos];
  return max(dfs1, dfs2);
}
int main() {
  cin >> time >> n;
  for (int i = 1; i <= n; i++) cin >> tcost[i] >> mget[i];
  cout << dfs(1, time) << endl;
  return 0;
}
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      tcost = [0] * 103
mget = [0] * 103

def dfs(pos, tleft):
    if pos == n + 1:
        return 0
    dfs1 = dfs2 = -INF
    dfs1 = dfs(pos + 1, tleft)
    if tleft >= tcost[pos]:
        dfs2 = dfs(pos + 1, tleft - tcost[pos]) + mget[pos]
    return max(dfs1, dfs2)

time, n = map(lambda x:int(x), input().split())
for i in range(1, n + 1):
    tcost[i], mget[i] = map(lambda x:int(x), input().split())
print(dfs(1, time))
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      // Make sure to add code blocks to your code group

      emmmmmm……还是 30 分。

      但这个时候，dfs 函数已经不需要借助任何外部变量了。

      # 优化二

      然后我非常无聊，将所有 dfs 的返回值都记录下来，竟然发现……

      对于相同的 pos 和 tleft，dfs 的返回值总是相同的！

      想一想也不奇怪，因为我们的 dfs 没有依赖任何外部变量。

      注：tcost、mget 这两个数组不算是外部变量，因为它们的值在 dfs 过程中不会被改变。

      然后？

      开个数组 mem, 记录下来每个 dfs(pos,tleft) 的返回值。刚开始把 mem 中每个值都设成 -1（代表没访问过）。每次刚刚进入一个 dfs 前（我们的 dfs 是递归调用的嘛），都判断 mem[pos][tleft] 是否为 -1, 如果是就正常执行并把答案记录到 mem 中，否则？

      直接返回 mem 中的值！

        int n, t;
int tcost[103], mget[103];
int mem[103][1003];
int dfs(int pos, int tleft) {
  if (mem[pos][tleft] != -1) return mem[pos][tleft];
  if (pos == n + 1) return mem[pos][tleft] = 0;
  int dfs1, dfs2 = -INF;
  dfs1 = dfs(pos + 1, tleft);
  if (tleft >= tcost[pos]) dfs2 = dfs(pos + 1, tleft - tcost[pos]) + mget[pos];
  return mem[pos][tleft] = max(dfs1, dfs2);
}
int main() {
  memset(mem, -1, sizeof(mem));
  cin >> t >> n;
  for (int i = 1; i <= n; i++) cin >> tcost[i] >> mget[i];
  cout << dfs(1, t) << endl;
  return 0;
}
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        18
        tcost = [0] * 103
mget = [0] * 103
mem = [[-1 for i in range(1003)] for j in range(103)]
def dfs(pos, tleft):
    if mem[pos][tleft] != -1:
        return mem[pos][tleft]
    if pos == n + 1:
        mem[pos][tleft] = 0
        return mem[pos][tleft]
    dfs1 = dfs2 = -INF
    dfs1 = dfs(pos + 1, tleft)
    if tleft >= tcost[pos]:
        dfs2 = dfs(pos + 1, tleft - tcost[pos]) + mget[pos]
    mem[pos][tleft] = max(dfs1, dfs2)
    return mem[pos][tleft]


t, n = map(lambda x:int(x), input().split())
for i in range(1, n + 1):
    tcost[i], mget[i] = map(lambda x:int(x), input().split())
print(dfs(1, t))
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        18
        19
        20
        21
        // Make sure to add code blocks to your code group

        此时 mem 的意义与 dfs 相同：

        在时间 tleft 内采集 后 pos 个草药，能获得的最大收益

        这能 AC？

        能。这就是“采药”那题的 AC 代码

        这就是记忆化搜索。

        # 总结

        记忆化搜索的特征：

        • 不依赖任何 外部变量
        • 答案以返回值的形式存在，而不能以参数的形式存在（就是不能将 dfs 定义成 dfs(pos,tleft,nowans)，这里面的 nowans 不符合要求）。
        • 对于相同一组参数，dfs 返回值总是相同的

        # 记忆化搜索与动态规划的关系：

        有人会问：记忆化搜索难道不是搜索？

        是搜索。但个人认为它更像 dp：

        不信你看 mem 的意义：

        在时间 tleft 内采集 后 pos 个草药，能获得的最大收益

        这不就是 dp 的状态？

        由上面的代码中可以看出：

        这不就是 dp 的状态转移？

        个人认为：

        记忆化搜索约等于动态规划，（印象中）任何一个 dp 方程都能转为记忆化搜索

        大部分记忆化搜索的状态/转移方程与 dp 都一样，时间复杂度/空间复杂度与 不加优化的 dp 完全相同

        比如：

        转为

          int dfs(int i, int j, int k) {
  // 判断边界条件
  if (mem[i][j][k] != -1) return mem[i][j][k];
  return mem[i][j][k] = dfs(i + 1, j + 1, k - a[j]) + dfs(i + 1, j, k);
}
int main() {
  memset(mem, -1, sizeof(mem));
  // 读入部分略去
  cout << dfs(1, 0, 0) << endl;
}
          1
          2
          3
          4
          5
          6
          7
          8
          9
          10
          def dfs(i, j, k):
    # 判断边界条件
    if mem[i][j][k] != -1:
        return mem[i][j][k]
    mem[i][j][k] = dfs(i + 1, j + 1, k - a[j]) + dfs(i + 1, j, k)
    return mem[i][j][k]
          1
          2
          3
          4
          5
          6
          // Make sure to add code blocks to your code group

          # 如何写记忆化搜索

          # 方法一

          1. 把这道题的 dp 状态和方程写出来
          2. 根据它们写出 dfs 函数
          3. 添加记忆化数组

          举例：

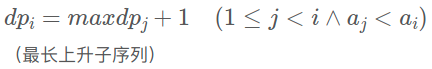
          image-20210910172025456

          （最长上升子序列）

          转为

            int dfs(int i) {
  if (mem[i] != -1) return mem[i];
  int ret = 1;
  for (int j = 1; j < i; j++)
    if (a[j] < a[i]) ret = max(ret, dfs(j) + 1);
  return mem[i] = ret;
}
int main() {
  memset(mem, -1, sizeof(mem));
  // 读入部分略去
  cout << dfs(n) << endl;
}
            1
            2
            3
            4
            5
            6
            7
            8
            9
            10
            11
            12
            def dfs(i):
    if mem[i] != -1:
        return mem[i]
    ret = 1
    for j in range(1, i):
        if a[j] < a[i]:
            ret = max(ret, dfs(j) + 1)
    mem[i] = ret
    return mem[i]
            1
            2
            3
            4
            5
            6
            7
            8
            9
            // Make sure to add code blocks to your code group

            # 方法二

            1. 写出这道题的暴搜程序（最好是 DFS)
            2. 将这个 dfs 改成“无需外部变量”的 dfs
            3. 添加记忆化数组

            举例：本文最开始介绍“什么是记忆化搜索”时举的“采药”那题的例子

            # 记忆化搜索的优缺点

            优点：

            • 记忆化搜索可以避免搜到无用状态，特别是在有状态压缩时

            举例：给你一个有向图（注意不是完全图），经过每条边都有花费，求从点 出发，经过每个点 恰好一次 后的最小花费（最后不用回到起点），保证路径存在。

            dp 状态很显然：

            设 表示身处在 处，走过 （一个表示各个节点的访问情况的二进制数）中的顶点后的最小花费

            常规 的状态数为 ，转移复杂度（所有的加在一起）为

            但是！如果我们用记忆化搜索，就可以避免到很多无用的状态，比如 为起点却已经经过了多于一个点的情况。

            • 不需要注意转移顺序（这里的“转移顺序”指正常 dp 中 for 循环的嵌套顺序以及循环变量是递增还是递减）

            举例：用常规 dp 写“合并石子”需要先枚举区间长度然后枚举起点，但记忆化搜索直接枚举断点（就是枚举当前区间由哪两个区间合并而成）然后递归下去就行

            • 边界情况非常好处理，且能有效防止数组访问越界
            • 有些 dp（如区间 dp) 用记忆化搜索写很简单但正常 dp 很难
            • 记忆化搜索天生携带搜索天赋，可以使用技能“剪枝”！

            缺点：

            • 致命伤：不能滚动数组！
            • 有些优化比较难加
            • 由于递归，有时效率较低但不至于 TLE（状压 dp 除外）

            # 记忆化搜索的注意事项

            • 千万别忘了加记忆化！（别笑，认真的）
            • 边界条件要加在检查当前数组值是否为非法数值（防止越界）
            • 数组不要开小了

            # 模板

            int g[MAXN];
int f(状态参数) {
  if (g[规模] != 无效数值) return g[规模];
  if (终止条件) return 最小子问题解;
  g[规模] = f(缩小规模);
  return g[规模];
}
int main() {
  // ...
  memset(g, 无效数值, sizeof(g));
  // ...
}
            1
            2
            3
            4
            5
            6
            7
            8
            9
            10
            11
            12

            如果你觉得我写的东西对你有用，想表示感谢的，扫下面的二维码吧😎。

            微信 支付宝 云闪付(国内银行APP也可)
            查看打赏名单
            上次更新: 2022/02/20, 16:31:14
            1.动态规划基础

            ←

            最近更新
            01
            认领打赏
            04-24
            02
            已认领打赏列表
            04-24
            03
            1283：登山
            03-11
            更多文章>
            Theme by Vdoing | Copyright © 2016-2023 极客分享

            皖ICP备15004818号-3